2010年03月29日
懐かしの?黄金分割
突然ですが、「黄金分割」をご存じですか?
総計の皆さん、日程分割の手法である「黄金分割法」のことではないですよ。
ちなみに「黄金分割法」の由来は、
穴を埋めてから日程分割 → AU(Ana wo Umete kara)分割 → (元素記号Auが金であることから)黄金分割
懐かしいですね。
それでは、下の図を見てください。

図のように辺AB上に点Cがあり、
(AC + CB):AC=AC:CB (つまり AB:AC=AC:CB)
が成り立つとき、「点Cは辺ABを黄金分割している」と言います。
このときの比AC:CBは黄金比と呼ばれ、最も美しい比であると言われています。
さて、Wikipediaの黄金比のページには、
要するに、下図のような正五角形があったとすると、AB:AC=AC:CBが成立しているということです。

ホンマかいな?ということで、これを証明してみたいと思います。
(興味のある方は、ぜひチャレンジしてみてください)
※予想より、はるかに長くなってしまった・・・覚悟して読んでね
総計の皆さん、日程分割の手法である「黄金分割法」のことではないですよ。
ちなみに「黄金分割法」の由来は、
穴を埋めてから日程分割 → AU(Ana wo Umete kara)分割 → (元素記号Auが金であることから)黄金分割
懐かしいですね。
それでは、下の図を見てください。

図のように辺AB上に点Cがあり、
(AC + CB):AC=AC:CB (つまり AB:AC=AC:CB)
が成り立つとき、「点Cは辺ABを黄金分割している」と言います。
このときの比AC:CBは黄金比と呼ばれ、最も美しい比であると言われています。
さて、Wikipediaの黄金比のページには、
幾何学的には黄金比は正五角形の中にみることができる。正五角形に対角線を引くと、その線分は互いに黄金比に分割する関係を取る。とあります。
要するに、下図のような正五角形があったとすると、AB:AC=AC:CBが成立しているということです。

ホンマかいな?ということで、これを証明してみたいと思います。
(興味のある方は、ぜひチャレンジしてみてください)
※予想より、はるかに長くなってしまった・・・覚悟して読んでね
まずは、この図形の角度やらなんやらを求めていきます。
元となっている図形は正五角形なので、
∠ADB=∠DBE=108°
と言えます。
また、三角形ABDと三角形BDEはそれぞれAD=BD、BD=BEである二等辺三角形なので、
∠ABD=∠BAD、∠BDE=∠BED
となります。
「三角形の内角の和は180°」であることから、
∠ABD=∠BAD=(180°-∠ADB)/2=(180°-108°)/2=36°
同様に、
∠BDE=∠BED=(180°-∠DBE)/2=(180°-108°)/2=36°
です。
次に、三角形BCDに注目します。
先ほど求めた角度から
∠CBD(=∠ABD)=∠BDC(=∠BDE)=36°
なので、三角形BCDはBC=CDである二等辺三角形であることが分かります。
さらに、三角形の内角の和より
∠BCD=180°-(∠CBD+∠BDC)=180°-(36°+36°)=108°
が求まります。
続いて、三角形ACDについて考えます。
辺ABは直線なので、
∠ACD+∠BCD=180°
が成り立ちます。
上で∠BCD=108°だったので、
∠ACD=180°-∠BCD=180°-108°=72°
となります。
まだ∠ADCが分かっていませんが、∠ACD=72°、∠CAD(=∠BAD)=36°、そして三角形の内角の和から
∠ADC=180°-(∠ACD+∠CAD)=180°-(72°+36°)=72°
です。
これより∠ACD=∠ADC=72°なので、三角形ACDはAC=ADの二等辺三角形であることが分かりました。
ここまでをまとめると、下図のようになります。

(疲れ始めてきたかもしれませんが、まだまだ続くよ~)
さて、ここで正五角形の一辺の長さを1とすると、AC=ADより
AC=AD=1
となります。
今回は「点Cが本当に辺ABを黄金分割しているのか?」を明らかにしようとしています。
このためには、AB:AC=AC:BCが成立していることを示せば良いわけです。
AB:AC=AC:BCであるとき、

が成立します。
先ほど決めたAC=AD=1をこの に代入すると、
に代入すると、

となります。
また、BC=AB-ACなので、AC=1より
BC=AB-1
です。
これを に代入してやると、
に代入してやると、

となり、この式が成り立っていることを示せば、「点Cは本当に辺ABを黄金分割している!」と言えるわけです。
これを示すためには、辺ABの長さを求める必要がありそうです。
なので、これより辺ABについて考えていきたいと思います。
点Dから辺ABに向かって垂線を降ろし、交わった点を点Fとします。

このとき、直角三角形の性質から、
AF=AD cos(36°)
が成り立ちます。
ここで、AD=1だったので、
AF=cos(36°)
となります。
同様にして、辺BFについても
BF=cos(36°)
と言えます。
つまり、
AB=AF+BF=cos(36°)+cos(36°)=2cos(36°)
となるわけです。
はて、ここで困ったぞと。
cos(36°)って、いったいどんな値になるの?
高校までの知識では、
・cos(0°)=1
・cos(30°)=√3/2
・cos(45°)=1/√2(=√2/2)
・cos(60°)=1/2
・cos(90°)=0
くらいしか分からん・・・。
しばらく悩んだ後、

なので、5倍角の公式を求めてみるかと考えるに至りました。
5倍角の公式とは、「sin5θやcos5θをsinθやcosθで表現すると〇〇になる」というものです。
ちなみに2倍角の公式は、


となります。
なんだか、見たことある気がしませんか?
5倍角の公式を求めるためには、三角関数の加法定理である


を用います。
こいつらを使ってゴニョゴニョやると、

を得ることができます。
次に考えなければならないのは、「求めたこの式に何を入れてやると良いか?」ということです。
試しにθ=36°としてみると、5θ=36°×5=180°なので、

となります。(cos(180°)=-1より)
うーん、これはなんだか微妙・・・。
やっぱり、cos5θ=0となってくれた方が、嬉しい気がする。
そんなわけで、すでに知っているcos(90°)=0を活かし、5θ=90°、つまりθ=18°とすることに。
θ=18°を5倍角の公式に代入すると、

が得られます。
ここからちょっと込み入った話になるのですが、
・余弦関数 cos x は、0 < x < π[←パイ]において狭義単調減少関数である(0 < x < π[←パイ]では、xが大きいほどcos xが小さくなる)こと
・0° < 18° < 90°であること
の2点から、
0 < cos(18°) < 1
を導くことができます。
これより、cos(18°)≠0なので、先ほど出てきた の両辺をcos(18°)で割っても問題ないと言えます。
の両辺をcos(18°)で割っても問題ないと言えます。
両辺をcos(18°)で割ると、

です。
(なんとなく、もうちょっとで解けそうな気がする!)
得られた式をじーっと見ていると、 とすれば
とすれば

となることに気が付きました。
これは、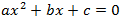 の形をしているため、解の公式である
の形をしているため、解の公式である

を用いて解くことができます。
もっとよくよく見ると、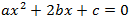 となっているので、さらに簡単な
となっているので、さらに簡単な

を適用可能です。
この公式に当てはめると、a=16、b=-10、c=5から

とすることができます。
よって、

となります。
ここで、0° < 18° < 30° < 90°のため、
0(=cos(90°)) < cos(30°) < cos(18°) < 1(=cos(0°))
であると言えます。
前述の通り、
0 < x < π[←パイ]ではxが大きいほどcos xが小さくなる
からです。
これをそれぞれ2乗すると、

となります。
より具体的な値を計算すると、

です。
 について、プラスの場合とマイナスの場合の値を求めると
について、プラスの場合とマイナスの場合の値を求めると


という結果が得られます。
2つのうち、 の条件に当てはまるのはプラスのものだけなので、
の条件に当てはまるのはプラスのものだけなので、

となります。
こうしてやっと、 について値を得ることができました。
について値を得ることができました。
しかし、欲しいのは2cos(36°)の値です。
ここで、2倍角の公式である

を思い出します。
θ=18°としてやれば、左辺はcos(36°)!
早速代入してやると、

となりました。( を利用)
を利用)
よって、

となるわけです。
これより、やっと

と、辺ABの長さを求めることができました。
さて、そろそろ最後の仕上げです。
ついに を示します。
を示します。
右辺を計算していって、左辺と等しくなればOKです。
計算は以下の通り。

以上から、

となることが分かりました。
これにより、「点Cは辺ABを黄金分割している」ということが証明できました。
やった!
ああ、長かった。
お疲れ様でした。
もっとラクな解き方思い付いたら、ぜひ教えてください。
あと、どっか間違ってたら、ご指摘お願いします。
まあ、わざわざ確かめる人もおらんやろうけどw
元となっている図形は正五角形なので、
∠ADB=∠DBE=108°
と言えます。
また、三角形ABDと三角形BDEはそれぞれAD=BD、BD=BEである二等辺三角形なので、
∠ABD=∠BAD、∠BDE=∠BED
となります。
「三角形の内角の和は180°」であることから、
∠ABD=∠BAD=(180°-∠ADB)/2=(180°-108°)/2=36°
同様に、
∠BDE=∠BED=(180°-∠DBE)/2=(180°-108°)/2=36°
です。
次に、三角形BCDに注目します。
先ほど求めた角度から
∠CBD(=∠ABD)=∠BDC(=∠BDE)=36°
なので、三角形BCDはBC=CDである二等辺三角形であることが分かります。
さらに、三角形の内角の和より
∠BCD=180°-(∠CBD+∠BDC)=180°-(36°+36°)=108°
が求まります。
続いて、三角形ACDについて考えます。
辺ABは直線なので、
∠ACD+∠BCD=180°
が成り立ちます。
上で∠BCD=108°だったので、
∠ACD=180°-∠BCD=180°-108°=72°
となります。
まだ∠ADCが分かっていませんが、∠ACD=72°、∠CAD(=∠BAD)=36°、そして三角形の内角の和から
∠ADC=180°-(∠ACD+∠CAD)=180°-(72°+36°)=72°
です。
これより∠ACD=∠ADC=72°なので、三角形ACDはAC=ADの二等辺三角形であることが分かりました。
ここまでをまとめると、下図のようになります。

(疲れ始めてきたかもしれませんが、まだまだ続くよ~)
さて、ここで正五角形の一辺の長さを1とすると、AC=ADより
AC=AD=1
となります。
今回は「点Cが本当に辺ABを黄金分割しているのか?」を明らかにしようとしています。
このためには、AB:AC=AC:BCが成立していることを示せば良いわけです。
AB:AC=AC:BCであるとき、

が成立します。
先ほど決めたAC=AD=1をこの
 に代入すると、
に代入すると、
となります。
また、BC=AB-ACなので、AC=1より
BC=AB-1
です。
これを
 に代入してやると、
に代入してやると、
となり、この式が成り立っていることを示せば、「点Cは本当に辺ABを黄金分割している!」と言えるわけです。
これを示すためには、辺ABの長さを求める必要がありそうです。
なので、これより辺ABについて考えていきたいと思います。
点Dから辺ABに向かって垂線を降ろし、交わった点を点Fとします。

このとき、直角三角形の性質から、
AF=AD cos(36°)
が成り立ちます。
ここで、AD=1だったので、
AF=cos(36°)
となります。
同様にして、辺BFについても
BF=cos(36°)
と言えます。
つまり、
AB=AF+BF=cos(36°)+cos(36°)=2cos(36°)
となるわけです。
はて、ここで困ったぞと。
cos(36°)って、いったいどんな値になるの?
高校までの知識では、
・cos(0°)=1
・cos(30°)=√3/2
・cos(45°)=1/√2(=√2/2)
・cos(60°)=1/2
・cos(90°)=0
くらいしか分からん・・・。
しばらく悩んだ後、

なので、5倍角の公式を求めてみるかと考えるに至りました。
5倍角の公式とは、「sin5θやcos5θをsinθやcosθで表現すると〇〇になる」というものです。
ちなみに2倍角の公式は、


となります。
なんだか、見たことある気がしませんか?
5倍角の公式を求めるためには、三角関数の加法定理である


を用います。
こいつらを使ってゴニョゴニョやると、

を得ることができます。
次に考えなければならないのは、「求めたこの式に何を入れてやると良いか?」ということです。
試しにθ=36°としてみると、5θ=36°×5=180°なので、

となります。(cos(180°)=-1より)
うーん、これはなんだか微妙・・・。
やっぱり、cos5θ=0となってくれた方が、嬉しい気がする。
そんなわけで、すでに知っているcos(90°)=0を活かし、5θ=90°、つまりθ=18°とすることに。
θ=18°を5倍角の公式に代入すると、

が得られます。
ここからちょっと込み入った話になるのですが、
・余弦関数 cos x は、0 < x < π[←パイ]において狭義単調減少関数である(0 < x < π[←パイ]では、xが大きいほどcos xが小さくなる)こと
・0° < 18° < 90°であること
の2点から、
0 < cos(18°) < 1
を導くことができます。
これより、cos(18°)≠0なので、先ほど出てきた
 の両辺をcos(18°)で割っても問題ないと言えます。
の両辺をcos(18°)で割っても問題ないと言えます。両辺をcos(18°)で割ると、

です。
(なんとなく、もうちょっとで解けそうな気がする!)
得られた式をじーっと見ていると、
 とすれば
とすれば
となることに気が付きました。
これは、
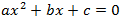 の形をしているため、解の公式である
の形をしているため、解の公式である
を用いて解くことができます。
もっとよくよく見ると、
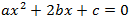 となっているので、さらに簡単な
となっているので、さらに簡単な
を適用可能です。
この公式に当てはめると、a=16、b=-10、c=5から

とすることができます。
よって、

となります。
ここで、0° < 18° < 30° < 90°のため、
0(=cos(90°)) < cos(30°) < cos(18°) < 1(=cos(0°))
であると言えます。
前述の通り、
0 < x < π[←パイ]ではxが大きいほどcos xが小さくなる
からです。
これをそれぞれ2乗すると、

となります。
より具体的な値を計算すると、

です。
 について、プラスの場合とマイナスの場合の値を求めると
について、プラスの場合とマイナスの場合の値を求めると

という結果が得られます。
2つのうち、
 の条件に当てはまるのはプラスのものだけなので、
の条件に当てはまるのはプラスのものだけなので、
となります。
こうしてやっと、
 について値を得ることができました。
について値を得ることができました。しかし、欲しいのは2cos(36°)の値です。
ここで、2倍角の公式である

を思い出します。
θ=18°としてやれば、左辺はcos(36°)!
早速代入してやると、

となりました。(
 を利用)
を利用)よって、

となるわけです。
これより、やっと

と、辺ABの長さを求めることができました。
さて、そろそろ最後の仕上げです。
ついに
 を示します。
を示します。右辺を計算していって、左辺と等しくなればOKです。
計算は以下の通り。

以上から、

となることが分かりました。
これにより、「点Cは辺ABを黄金分割している」ということが証明できました。
やった!
ああ、長かった。
お疲れ様でした。
もっとラクな解き方思い付いたら、ぜひ教えてください。
あと、どっか間違ってたら、ご指摘お願いします。
まあ、わざわざ確かめる人もおらんやろうけどw
Posted by wasese at 23:21│Comments(2)│独り言
この記事へのコメント
最初の方で色々と角度求めたとき、
その時点で、三角形DABと三角形CBDが相似って分る
(3つの角度が同じだから)。
ってことは、対応する辺の比は等しいから、
AB:AD=BD:BC ・・・・ア
一方で、三角形ACDは二等辺三角形だから、
AD=AC ・・・・イ
さらに、正五角形だから、
BD=AD ・・・・ウ
アイウの三点から、
AB:AC=AC:BC
その時点で、三角形DABと三角形CBDが相似って分る
(3つの角度が同じだから)。
ってことは、対応する辺の比は等しいから、
AB:AD=BD:BC ・・・・ア
一方で、三角形ACDは二等辺三角形だから、
AD=AC ・・・・イ
さらに、正五角形だから、
BD=AD ・・・・ウ
アイウの三点から、
AB:AC=AC:BC
Posted by 123 at 2010年03月30日 23:52
>123さん
確かに相似を使うと、あっという間ですね。
ありがとうございます。
確かに相似を使うと、あっという間ですね。
ありがとうございます。
Posted by s_wase at 2010年03月31日 00:05
at 2010年03月31日 00:05
 at 2010年03月31日 00:05
at 2010年03月31日 00:05コメントフォーム